
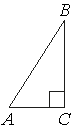
 В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Так как ∠С=90°, то треугольник ABC -
прямоугольный.
Следовательно:
sinB=AC/AB=6/10=0,6 (по определению).
Ответ: 0,6
Поделитесь решением
Присоединяйтесь к нам...
 Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
 Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
 Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды
CD, если AB=12, CD=16, а расстояние от центра окружности до хорды AB равно 8.
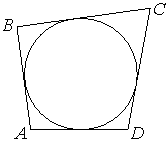 Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.





Комментарии: