ОГЭ, Математика. Геометрия: Задача №E41C75 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Геометрия: Задача №E41C75

Задача №891 из 1087
Условие задачи:

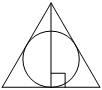
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.

Решение задачи:

По свойству равностороннего треугольника:

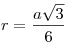
Тогда:
6r=a√3
a=6r/√3=6*5/√3= 30/√3=(3*10)/√3=((√3)²*10)/√3=10√3
По второму свойству равностороннего треугольника высота так же является и медианой.
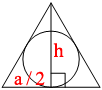Следовательно, она делит сторону, на которую опирается, пополам.
К тому же высота образует прямоугольный треугольник, следовательно, можно воспользоваться теоремой Пифагора:
a²=h²+(a/2)²
(10√3)²=h²+(10√3/2)²
100*3=h²+(5√3)²
300=h²+25*3
h²=300-75=225
h=√225=15
Ответ: 15

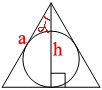Можно вместо теоремы Пифагора воспользоваться косинусом:
cosα=h/a (по определению).
По первому свойству равностороннего треугольника все углы равны 60°.
А по второму свойству, высота так же является и биссектрисой, т.е. делит угол пополам, следовательно α=60°/2=30°
По таблице косинусов:
√3/2=h/10√3
√3*10√3=2h
(√3)²*10=2h
3*10=2h
h=15
Ответ: 15

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №1BB912

В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.

Задача №8316E3

В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 65°. Найдите величину угла OCD.

Задача №F9DE8F

Высота равностороннего треугольника равна 96√3. Найдите его периметр.

Задача №0171FD

Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?

Задача №745683

Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Синус, косинус, тангенс и котангенс угла прямоугольного треугольника.

Синус равен отношению противолежащего катета к гипотенузе.
Sin α =

Косинус равен отношению прилежащего катета к гипотенузе.
Cos α =

Тангенс равен отношению противолежащего катета к прилежащему.
Tg α =

Котангенс равен отношению прилежащего катета к противолежащему.
Ctg α =

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.