
 В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
По
определению тангенса:
tgB=AC/BC
3/4=AC/12
AC=(3*12)/4=3*3=9
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BKC.
 В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
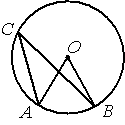 Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
 В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
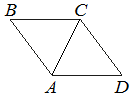 В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.





Комментарии: