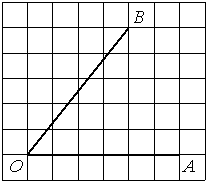
Найдите тангенс угла AOB, изображённого
на рисунке.
Проведем высоту из точки В к отрезку OA, чтобы получился
прямоугольный треугольник:
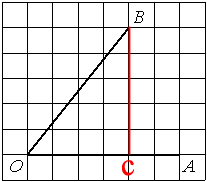Получился треугольник OBC с катетами ОС (длина 4) и BC (длина 5).
По определению тангенса:
tgAOB=BC/OC=5/4=1,25
Ответ: 1,25
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен 
. Найдите sinA.
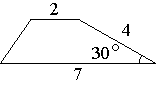Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: