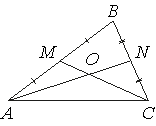
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=33, CM=15. Найдите ON.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
AO/ON=2/1, т.е. AO=2ON
При этом AN=AO+ON
33=AO+ON, подставляем в это уравнение первое равенство:
33=2ON+ON
33=3ON
ON=11
Ответ: 11
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая проходит 11°?
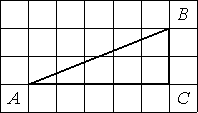Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
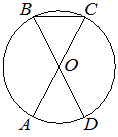В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: