
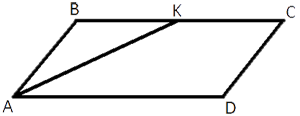 Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
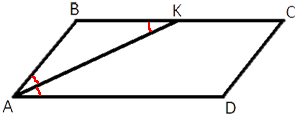 Стороны AD и BC параллельны по
определению параллелограмма.
Стороны AD и BC параллельны по
определению параллелограмма.
Тогда АК мы можем рассмотривать как секущую.
Тогда ∠DAK=∠BKA (так как они
накрест-лежащие).
ВК - вдвое меньше BC (т.к. К - середина).
AB тоже вдвое меньше BC (по условию).
Следовательно, BK=AB, т.е. треугольник ABK равнобедренный.
Тогда, по свойству равнобедренного треугольника, ∠BAK=∠BKA.
Получается, что ∠BAK=∠BKA=∠DAK.
Т.е. AK - биссектрисса.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь прямоугольного треугольника равна 2450√
Площадь прямоугольного треугольника равна 2450√
 Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
Какое наибольшее число коробок в форме прямоугольного параллелепипеда размером 30x50x90 (см) можно поместить в кузов машины размером 2,4x3x2,7 (м)?
 Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=12, CP=15, DP=25. Найдите AP.
 Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.



Комментарии: