
 Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
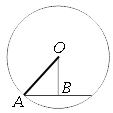 Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Рассмотрим треугольник AOB.
Данный треугольник
прямоугольный, так как расстояние ОВ является
высотой (кротчайшее расстояние).
AB равна половине длины
хорды (по
третьему свойству хорды).
Тогда, по
теореме Пифагора:
AO2=OB2+AB2
AO2=722+(130/2)2
AO2=5184+4225=9409
AO=97 - это радиус окружности, следовательно, диаметр:
D=2*AO=2*97=194
Ответ: 194
Поделитесь решением
Присоединяйтесь к нам...
 Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=25° (см. рисунок). Найдите величину угла AOB (в градусах).
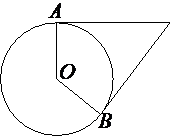 Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
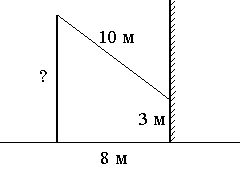 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
 Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите ∠C, если ∠A=81°. Ответ дайте в градусах.
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 80°. Найдите величину угла OAB.



Комментарии:
(2024-05-16 18:52:08) Милана: Дана окружность с центром О, через который проходят две хорды. Найди < D AB, если