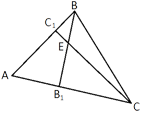Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
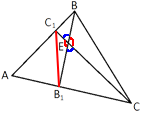Проведем отрезок B1C1 и рассмотрим треугольники EB1C и EC1B.
∠C1EB=∠B1EC (так как они
вертикальные).
∠EB1C=∠EC1B=90° (так как BB1 и CC1 -
высоты).
По
первому признаку подобия треугольников, рассматриваемые треугольники
подобны.
Следовательно:
EB1/EC1=EC/EB
Рассмотрим треугольники EС1B1 и ECB
∠BEC=∠B1EC1 (так как они
вертикальные).
Как мы выяснили ранее:
EB1/EC1=EC/EB
Умножим левую и правую части равенства на EC1, получим:
EB1=EC1*EC/EB
Разделим левую и правую части на EC, получаем:
EB1/EC=EC1/EB
Получается, что по
второму признаку подобия треугольников, треугольники EС1B1 и ECB
подобны.
Следовательно, по
определению, углы BB1C1 и BCC1 равны.
Поделитесь решением
Присоединяйтесь к нам...
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
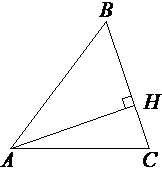В остроугольном треугольнике ABC высота AH равна 20√
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Треугольник со сторонами 1, 2, 4 не существует.
3) Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: