
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ550 –Є–Ј 1087 |
 –Э–∞–є–і–Є—В–µ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є —Г–≥–ї—Л ABC –Є BCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 60¬∞ –Є 135¬∞, –∞ CD=36.
–Э–∞–є–і–Є—В–µ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB —В—А–∞–њ–µ—Ж–Є–Є ABCD, –µ—Б–ї–Є —Г–≥–ї—Л ABC –Є BCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 60¬∞ –Є 135¬∞, –∞ CD=36.
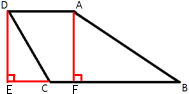 –Ф–Њ—З–µ—А—В–Є–Љ –Њ—В—А–µ–Ј–Ї–Є –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Ф–Њ—З–µ—А—В–Є–Љ –Њ—В—А–µ–Ј–Ї–Є –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
DE=AF, —В.–Ї. —Н—В–Њ
–≤—Л—Б–Њ—В—Л
—В—А–∞–њ–µ—Ж–Є–Є.
∠DCE=180¬∞-∠BCD=180¬∞-135¬∞=45¬∞ (—В.–Ї. —Н—В–Њ
—Б–Љ–µ–ґ–љ—Л–µ —Г–≥–ї—Л).
sin(∠DCE)=ED/CD (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О)
sin45¬∞=ED/CD (sin45¬∞=√
√
ED=36√
sin(∠ABF)=AF/AB (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О)
sin60°=ED/AB
AB=ED/sin60¬∞ (sin60¬∞=√
AB=(18√
–Ю—В–≤–µ—В: AB=12√
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–Ъ–∞–Ї–Є–µ –Є–Ј —Б–ї–µ–і—Г—О—Й–Є—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є –≤–µ—А–љ—Л?
1) –Х—Б–ї–Є –і–≤–∞ —Г–≥–ї–∞ –Њ–і–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л –і–≤—Г–Љ —Г–≥–ї–∞–Љ –і—А—Г–≥–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–Њ —В–∞–Ї–Є–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є –њ–Њ–і–Њ–±–љ—Л.
2) –Ф–Є–∞–≥–Њ–љ–∞–ї–Є —А–Њ–Љ–±–∞ —А–∞–≤–љ—Л.
3) –Ґ–∞–љ–≥–µ–љ—Б –ї—О–±–Њ–≥–Њ –Њ—Б—В—А–Њ–≥–Њ —Г–≥–ї–∞ –Љ–µ–љ—М—И–µ –µ–і–Є–љ–Є—Ж—Л.
 –Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є BC –Є AD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ O, BC=6, AD=13, AC=38. –Э–∞–є–і–Є—В–µ AO.
–Ф–Є–∞–≥–Њ–љ–∞–ї–Є AC –Є BD —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є BC –Є AD –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ O, BC=6, AD=13, AC=38. –Э–∞–є–і–Є—В–µ AO.
 –Э–∞ –Ї–∞–Ї–Њ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є (–≤ –Љ–µ—В—А–∞—Е) –Њ—В —Д–Њ–љ–∞—А—П —Б—В–Њ–Є—В —З–µ–ї–Њ–≤–µ–Ї —А–Њ—Б—В–Њ–Љ 2 –Љ, –µ—Б–ї–Є –і–ї–Є–љ–∞ –µ–≥–Њ —В–µ–љ–Є —А–∞–≤–љ–∞ 1 –Љ, –≤—Л—Б–Њ—В–∞ —Д–Њ–љ–∞—А—П 9 –Љ?
–Э–∞ –Ї–∞–Ї–Њ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є (–≤ –Љ–µ—В—А–∞—Е) –Њ—В —Д–Њ–љ–∞—А—П —Б—В–Њ–Є—В —З–µ–ї–Њ–≤–µ–Ї —А–Њ—Б—В–Њ–Љ 2 –Љ, –µ—Б–ї–Є –і–ї–Є–љ–∞ –µ–≥–Њ —В–µ–љ–Є —А–∞–≤–љ–∞ 1 –Љ, –≤—Л—Б–Њ—В–∞ —Д–Њ–љ–∞—А—П 9 –Љ?
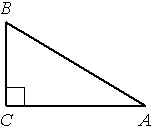 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=4, sinA=0,8. –Э–∞–є–і–Є—В–µ AB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=4, sinA=0,8. –Э–∞–є–і–Є—В–µ AB.
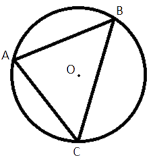 –Т–µ—А—И–Є–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –і–µ–ї—П—В –Њ–њ–Є—Б–∞–љ–љ—Г—О –Њ–Ї–Њ–ї–Њ –љ–µ–≥–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –љ–∞ —В—А–Є –і—Г–≥–Є, –і–ї–Є–љ—Л –Ї–Њ—В–Њ—А—Л—Е –Њ—В–љ–Њ—Б—П—В—Б—П –Ї–∞–Ї 3:4:11. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є –Љ–µ–љ—М—И–∞—П –Є–Ј —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–∞ 14.
–Т–µ—А—И–Є–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –і–µ–ї—П—В –Њ–њ–Є—Б–∞–љ–љ—Г—О –Њ–Ї–Њ–ї–Њ –љ–µ–≥–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М –љ–∞ —В—А–Є –і—Г–≥–Є, –і–ї–Є–љ—Л –Ї–Њ—В–Њ—А—Л—Е –Њ—В–љ–Њ—Б—П—В—Б—П –Ї–∞–Ї 3:4:11. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –µ—Б–ї–Є –Љ–µ–љ—М—И–∞—П –Є–Ј —Б—В–Њ—А–Њ–љ —А–∞–≤–љ–∞ 14.



–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: