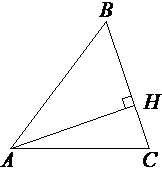
В остроугольном треугольнике ABC высота AH равна 20√
Треугольник ABH
прямоугольный, т.к. AH -
высота.
Тогда по
теореме Пифагора:
AB2=AH2+BH2
402=(20√
1600=400*3+BH2
400=BH2
BH=20
По
определению:
cos∠B=BH/AB=20/40=1/2=0,5
Ответ: cos∠B=0,5
Поделитесь решением
Присоединяйтесь к нам...
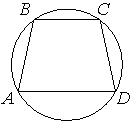Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-12-15 15:59:07) хуесос: )))