В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
Так как BM -
медиана, значит AM=MC=AC/2=79/2=39,5
Рассмотрим треугольник MBC.
Т.к. BC=BM (по условию задачи), значит этот треугольник
равнобедренный, BH -
высота этого треугольника. По
третьему свойству равнобедренного треугольника MH=HC=MC/2=39,5/2=19,75
Искомая AH=AC-HC=79-19,75=59,25
Ответ: AH=59,25
Поделитесь решением
Присоединяйтесь к нам...
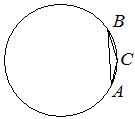В треугольнике ABC угол C равен 150°, AB=4. Найдите радиус окружности, описанной около этого треугольника.
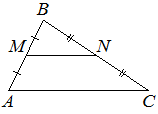Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
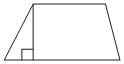Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: