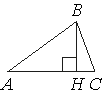В остроугольном треугольнике ABC проведена высота BH, ∠BAC=37°. Найдите угол ABH. Ответ дайте в градусах.
Рассмотрим треугольник ABH.
Это
прямоугольный треугольник, так как BH -
высота.
Тогда, по теореме о сумме углов треугольника:
180°=∠ABH+∠AHB+∠BAH
∠BAH=∠BAC=37° (так как это один и тот же угол).
180°=∠ABH+90°+37°
180°-90°-37°=∠ABH
∠ABH=53°
Ответ: 53
Поделитесь решением
Присоединяйтесь к нам...
Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 6. Найдите площадь трапеции.
Лестница соединяет точки A и B. Высота каждой ступени равна 10,5 см, а длина – 36 см. Расстояние между точками A и B составляет 15 м. Найдите высоту, на которую поднимается лестница (в метрах).
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: