Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Вариант №1 (Предложил пользователь Елена)
Проведем отрезок MP, как показано на рисунке. BM - диаметр малой окружности (по условию задачи), следовательно треугольник BMP -
прямоугольный с гипотенузой BM (по
свойству описанной окружности).
К тому же, по условию задачи, точка Р - середина стороны BC, т.е. BM -
серединный перпендикуляр к стороне BC.
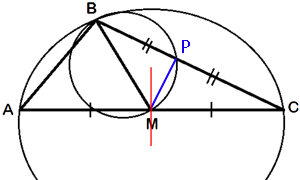Проведем
серединный перпендикуляр к стороне AC, как показано на рисунке.
Центр
описанной окружности совпадает с точкой пересечения
серединных перпендикуляров треугольника, а в данном случае - это точка М, т.е. точка М и есть центр
описанной окружности.
Так как получилось, что центр окружности лежит на стороне описываемого треугольника, то AM и MC - радиусы данной окружности и равны R=AC/2=4/2=2.
Ответ: 2
Поделитесь решением
Присоединяйтесь к нам...
Косинус острого угла A треугольника ABC равен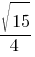 
. Найдите sinA.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: