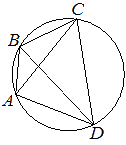Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
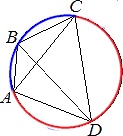∠ABC является вписанным углом и опирается на дугу ADC (красная).
Следовательно, по теореме о вписанном угле, градусная мера дуги ADC равна 138°*2=276°
Тогда градусная мера синей дуги равна 360°-276°=84°
∠ADC тоже является вписанным углом и опирается на дугу ABC (синяя).
Следовательно, по той же теореме о вписанном угле∠ADC=84°/2=42°.
Рассмотрим треугольник ACD.
По теореме о сумме углов треугольника запишем:
180°=∠ADC+∠CAD+∠ACD
180°=42°+83°+∠ACD
180°-42°-83°=∠ACD
∠ACD=55°
Заметим, что углы ACD и ABD являются вписанными и опираются на одну и ту же дугу.
Следовательно, эти углы равны, ∠ACD=∠ABD=55°
Ответ: 55
Поделитесь решением
Присоединяйтесь к нам...
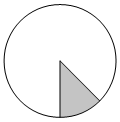Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
Какие из данных утверждений верны? Запишите их номера.
1) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
2) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны.
3) У равнобедренного треугольника есть центр симметрии.
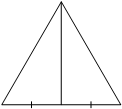Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника AKM к площади четырёхугольника KPCM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: