В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
Рассмотрим треугольник ABL.
∠BLA=180°-∠ALC=180°-52°=128° (т.к. это
смежные углы)
По
теореме о сумме углов треугольника:
180°=∠ABC+∠BLA+∠LAB=13°+128°+∠LAB
∠LAB=180°-13°-128°=39°
Рассмотрим треугольник ALC.
∠LAC=∠LAB=39° (т.к. AL -
биссектриса)
По
теореме о сумме углов треугольника:
180°=∠ALC+∠ACB+∠LAC=52°+∠ACB+39°
∠ACB=180°-52°-39°=89°
Ответ: 89
Поделитесь решением
Присоединяйтесь к нам...
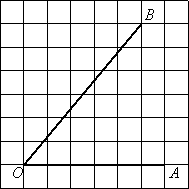Найдите тангенс угла AOB.
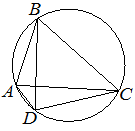Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
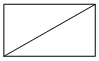В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
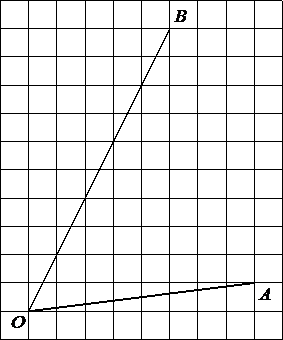Найдите тангенс угла
AOB.
Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: