
 В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
Продлим стороны AB и CD до пересечения друг с другом.
 Рассмотрим треугольник AED.
Рассмотрим треугольник AED.
По
теореме о сумме углов треугольника:
180°=∠EDA+∠DAE+∠AED
180°=90°+∠AED
∠AED=90°
Следовательно треугольник AED -
прямоугольный.
Рассмотрим треугольники AED и BEC.
∠AED - общий
∠EBC=∠EAD (т.к. это
соответственные углы)
Треугольники AED и BEC
подобны (по
первому признаку подобия треугольников).
Тогда по
определению подобия:
AD/BC=AE/BE
AD/BC=(AB+BE)/BE
49/21=(20+BE)/BE
49BE/21=20+BE
28BE/21=20
BE=20*21/28=15
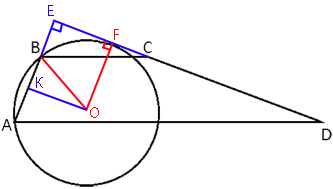 Обозначим точку F - точку касания прямой CD и окружности.
Обозначим точку F - точку касания прямой CD и окружности.
OF - искомый радиус окружности. Он перпендикулярен касательной EC (по
свойству касательной).
Проведем отрезок ОК перпендикулярно АВ.
OK - серединный перпендикуляр к
хорде AB (
третье свойство хорды)
Получается, что BK=AB/2=20/2=10.
EK=BE+BK=15+10=25
EK=OF=R=25, так как OKEF - прямоугольник.
Ответ: 25
Поделитесь решением
Присоединяйтесь к нам...
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=11°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=11°. Найдите угол NMB. Ответ дайте в градусах.
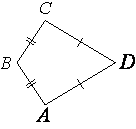 В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD известно, что AB=BC, AD=CD, ∠B=133°, ∠D=173°. Найдите
угол A. Ответ дайте в градусах.
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
 На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 9 и 6. Найдите площадь параллелограмма ABCD.
Комментарии:
(2018-01-19 21:22:57) Администратор: Евгений Бакин, согласен с Вами. Решение упрощено по Вашему варианту.
(2017-12-29 11:41:46) Евгений Бакин: Проще найти сразу OF=EK=EB+BK=15+10=25