
 Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
 Проведем отрезок CO.
Проведем отрезок CO.
Рассмотрим треугольник ACO.
∠ACO=∠ACB/2=82°/2=41° (по
второму свойству касательной).
∠CAO=90° (по
первому свойству касательной)
По
теореме о сумме углов треугольника:
180°=∠AOC+∠ACO+∠CAO
180°=∠AOC+41°+90°
∠AOC=49°
Рассмотрим треугольники ACO и BCO.
OC - общая сторона
AC=BC (по
второму свойству касательной)
OA=OB (т.к. это радиусы)
Следовательно, по
третьему признаку, данные треугольники равны.
Тогда и ∠AOC=∠BOC=49°
Рассмотрим треугольник AOB.
OA=OB (т.к. это радиусы)
Следовательно, треугольник AOB -
равнобедренный.
Тогда ∠BAO=∠ABO (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OAB+∠ABO
180°=∠AOC+∠BOC+2∠ABO
180°=49°+49°+2∠ABO
82°=2∠ABO
∠ABO=41°
Ответ: 41
Поделитесь решением
Присоединяйтесь к нам...
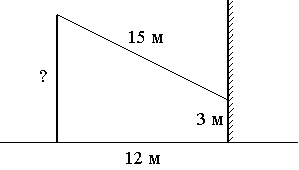 От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
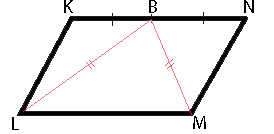 В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
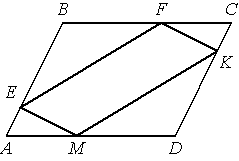 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
Комментарии: