
 AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
Рассмотри треугольник OCB.
OB=OC (т.к. это радиусы)
Следовательно, треугольник OCB -
равнобедренный.
Тогда ∠ACB=∠CBD=74° (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠ACB+∠CBD+∠BOC
180°=74°+74°+∠BOC
∠BOC=32°
∠BOC=∠AOD=32° (т.к. они
вертикальные).
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 17:10, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
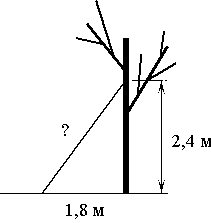 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 1,8 м?
 На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
Комментарии: