
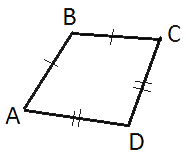
 В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
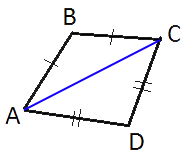 Проведем диагональ AC.
Проведем диагональ AC.
Рассмотрим треугольник ABC.
Так как AB=BC, значит треугольник ABC -
равнобедренный.
По
теореме о сумме углов треугольника:
180°=∠B+∠BAC+∠BCA.
180°=100°+∠BAC+∠BCA.
80°=∠BAC+∠BCA.
По
свойству равнобедренного треугольника, ∠BAC=∠BCA, тогда
∠BAC=∠BCA=80°/2=40°.
Треугольник ACD тоже
равнобедренный.
Аналогичными вычислениями получаем:
180°=104°+∠DAC+∠DCA.
∠DAC+∠DCA=76°/2=38°
∠A=∠BAC+∠CAD=40°+38°=78°
Ответ: 78
Поделитесь решением
Присоединяйтесь к нам...
 Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
 Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
 Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Синус острого угла A треугольника ABC равен 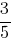 . Найдите CosA.
. Найдите CosA.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Комментарии: