Укажите номера верных утверждений.
1) Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Квадрат является прямоугольником.
3) Сумма углов любого треугольника равна
180°.
Рассмотрим каждое утверждение:
1) "Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника".
Высота, проведенная к основанию является и
медианой, и биссектрисой (по
свойству равнобедренного треугольника), т.е. является
серединным перпендикуляром. А центром описанной окружности является точка пересечения
серединных перпендикуляров (
теорема об описанной окружности). Следовательно, это утверждение верно.
2) "Квадрат является прямоугольником", это утверждение верно (по
определению).
3) "Сумма углов любого треугольника равна 180°", это утверждение верно (по
теореме).
Поделитесь решением
Присоединяйтесь к нам...
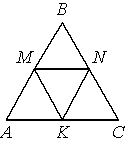В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: