
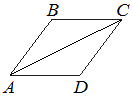
 В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
В ромбе ABCD угол ABC равен 146°. Найдите угол ACD. Ответ дайте в градусах.
Рассмотрим треугольник ABC.
AB=BC (по определению ромба).
Следовательно, треугольник ABC -
равнобедренный.
∠CAB=∠ACB (по свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠CAB+∠ACB+∠ABC
180°=∠ACB+∠ACB+146°
180°-146°=2*∠ACB
34°=2*∠ACB
∠ACB=17°
Рассмотрим треугольники ABC и ADC:
1) AB=BC=CD=DA (по определению ромба).
2) AC - общая сторона.
Тогда по 3-му признаку данные треугольники равны.
Следовательно:
∠ACD=∠ACB=17°
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Каждая из биссектрис равнобедренного треугольника является его высотой.
2) Диагонали прямоугольника равны.
3) У любой трапеции основания параллельны.
 Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
 Радиус вписанной в квадрат окружности равен 14√
Радиус вписанной в квадрат окружности равен 14√
 В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
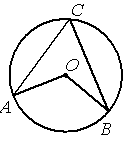 Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
Комментарии: