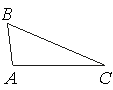
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
По
теореме косинусов:
AC2=AB2+BC2-2*AB*BC*cos∠ABC
72=32+82-2*3*8*cos∠ABC
49=9+64-48*cos∠ABC
49-9-64=-48*cos∠ABC
-24=-48*cos∠ABC |:(-24)
1=2*cos∠ABC
cos∠ABC=1/2=0,5
Ответ: 0,5
Поделитесь решением
Присоединяйтесь к нам...
Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные
25° и 100° соответственно.
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
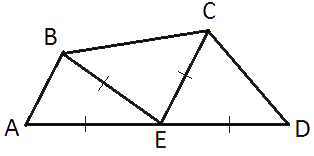Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: