
 Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10√3. Найдите длину стороны этого треугольника.
Вариант №1 (Для тех, кто помним формулу)
По
третьему свойству равностороннего треугольника:
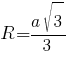
3R=a√3
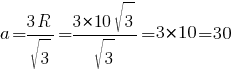
Ответ: 30

Поделитесь решением
Присоединяйтесь к нам...
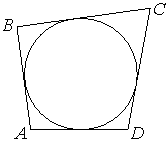 Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
Четырёхугольник ABCD описан около окружности, AB=9, BC=13, CD=18. Найдите AD.
 В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
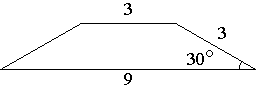 Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
 Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
Радиус окружности, вписанной в прямоугольную трапецию, равен 18. Найдите высоту этой трапеции.
 Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
Комментарии: