
 Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
По
первому свойству равностороннего треугольника, все его углы равны 60°.
По
теореме синусов:
2R=a/sin60
a=2R*sin60= (найдем sin60 по таблице)
=2*10*√3/2=10√3
По второму свойству равностороннего треугольника, высота равна:
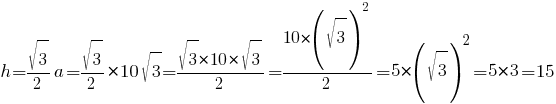
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
 Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
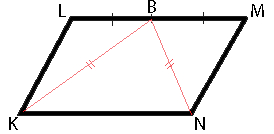 В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
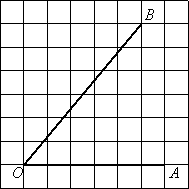 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
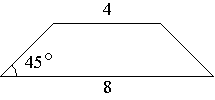 В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 26:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 7.
Комментарии: