Синус острого угла A треугольника ABC равен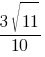 
. Найдите CosA.
Так как нам ничего не известно про треугольник ABC, прямоугольный он или нет и т.д. То остается только воспользоваться
основной тригонометрической формулой:
sin2A+cos2A=1
По
второму правилу действий со степенями:
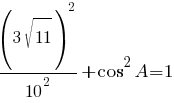
Применим
первое правило действий со степенями для числителя:
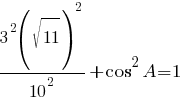
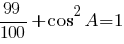
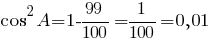
cosA=√0,01=0,1
Ответ: 0,1
Поделитесь решением
Присоединяйтесь к нам...
Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: