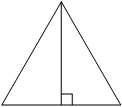
Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
В равностороннем треугольнике все стороны равны, пусть стороны равны "а".
По свойству равностороннего треугольника высота так же является и медианой, т.е. делит сторону по полам.
Треугольники, которые образует высота, являются прямоугольными.
Следовательно, к ним можно применить теорему Пифагора:
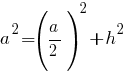
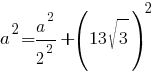
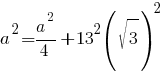
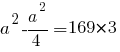
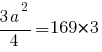
3a2=4*169*3 |:3
a2=4*169
a2=676
a=√676=26
Ответ: 26
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
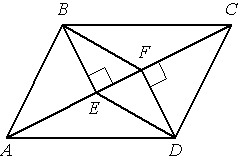В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=21, BF=20.
Радиус вписанной в квадрат окружности равен 14√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: