Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Отрезки AN и CM - являются
медианами треугольника ABC.
Тогда, применяя первое свойство медианы, можем записать:
AO/ON=2/1, т.е. ON=AO/2
При этом AN=AO+ON
27=AO+ON, подставляем в это уравнение первое равенство:
27=AO+AO/2 |*2
54=2AO+AO
54=3AO
AO=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
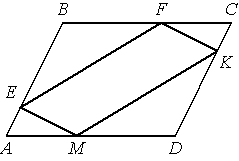В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
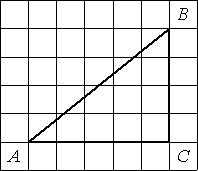Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Площадь прямоугольного треугольника равна
338√
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: