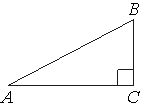
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Так как ∠С=90°, то треугольник ABC -
прямоугольный.
Следовательно:
sinB=AC/AB=4/5=0,8 (по определению).
Ответ: 0,8
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь трапеции, изображённой на рисунке.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 7.
В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Радиус вписанной в квадрат окружности равен 24√2. Найдите радиус окружности, описанной около этого квадрата.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: