В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
Легче всего воспользоваться формулой нахождения площади треугольника
через две стороны и угол между ними:
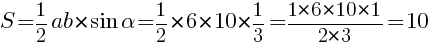
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-12-11 12:41:17) Администратор: Из условия, синус альфа равен 1/3.
(2018-12-10 13:16:16) : откуда 1\\3