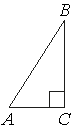
В треугольнике ABC угол C равен 90°, AC=6, AB=10. Найдите sinB.
Так как ∠С=90°, то треугольник ABC -
прямоугольный.
Следовательно:
sinB=AC/AB=6/10=0,6 (по определению).
Ответ: 0,6
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
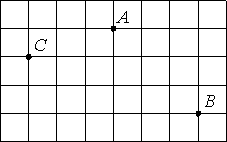На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: