
Косинус острого угла А треугольника равен 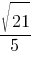 . Найдите sinA.
. Найдите sinA.
Воспользуемся основной тригонометрической формулой:
sin2A+cos2A=1
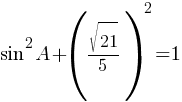
По
второму правилу работы со степенями:
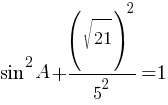
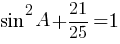
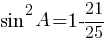
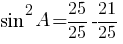
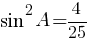
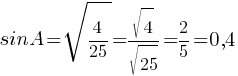
Ответ: 0,4
Поделитесь решением
Присоединяйтесь к нам...
 Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
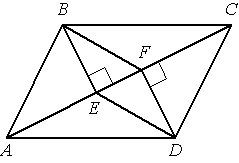 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
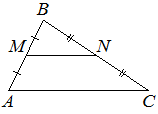 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Комментарии:
(2023-10-27 20:07:34) : 6F6C4D
(2023-10-27 20:06:38) : 6F6C4D