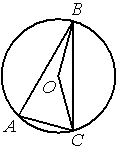
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
По условию ∠BOC=160°, этот угол является
центральным, соответственно дуга ВC (малая часть) тоже равна 160°.
∠BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, ∠BAC=160°/2=80°.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
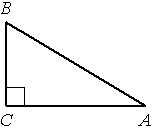В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
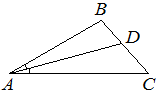В треугольнике ABC известно, что ∠BAC=28°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
Синус острого угла A треугольника ABC равен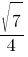 
. Найдите CosA.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: