
 Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
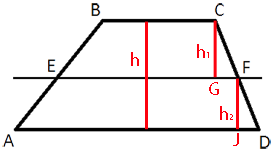 Проведем
высоты h1 и h2 как показано на рисунке.
Проведем
высоты h1 и h2 как показано на рисунке.
Рассмотрим треугольники CFG и FDJ.
∠CGF=∠FJD=90° (т.к. мы проводили
высоты).
∠CFG=∠FDJ (т.к. это
соответственные углы).
Следовательно, эти треугольники
подобны по
первому признаку подобия.
По
определению подобных треугольников:
CF/DF=CG/FJ=4/3
Для простоты обозначим:
CG=h1
FJ=h2
SEBCF=(CB+EF)*h1/2
SAEFD=(EF+AD)*h2/2
SABCD=(BC+AD)*(h1+h2)/2
Так сумма площадей этих
трапеций равна площади большой трапеции, то запишем:
(CB+EF)*h1/2+(EF+AD)*h2/2=(BC+AD)*(h1+h2)/2
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2)
CB*h1+EF*h1+EF*h2+AD*h2=BC*h1+BC*h2+AD*h1+AD*h2
CB*h1+EF*h1-BC*h1-AD*h1=BC*h2+AD*h2-EF*h2-AD*h2
(CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2
(EF-AD)*h1=(BC-EF)*h2
h1/h2=(BC-EF)/(EF-AD)
4/3=(14-EF)/(EF-42)
4(EF-42)=3(14-EF)
4*EF-168=42-3*EF
7*EF=210
EF=30
Ответ: EF=30
Поделитесь решением
Присоединяйтесь к нам...
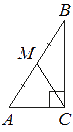 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=60, BC=40. Найдите CM.
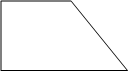 Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
Тангенс острого угла прямоугольной трапеции равен 5/3. Найдите её большее основание, если меньшее основание равно высоте и равно 40.
 В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
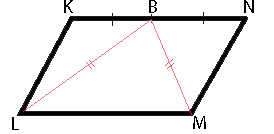 В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
 Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
Комментарии: