Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
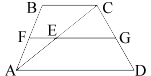Обозначим ключевые точки, как показано на рисунке.
Рассмотрим треугольник ABC.
AF=FB (по
определению средней линии трапеции).
Тогда, по теореме Фалеса:
AE=EC
Получается, что FE -
средняя линия треугольника ABC.
FE=BC/2=8/2=4 (по
теореме о средней линии треугольника).
Рассмотрим треугольник ACD.
Аналогично, EG -
средняя линия данного треугольника, следовательно EG=AD/2=18/2=9.
Ответ: 9
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
Радиус вписанной в квадрат окружности равен 7√
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: