Сумма двух углов равнобедренной трапеции равна 50°. Найдите больший угол трапеции. Ответ дайте в градусах.
В задаче не сказано, сумма каких углов равна 50°, поэтому это надо определить исходя из знаний и логики.
Предположим, что это углы при одной из боковых сторон трапеции.
Тогда это
внутренние односторонние углы при параллельных прямых (основаниях трапеции) и секущей - боковой стороне, сумма таких углов равна 180°, т.е. это предположение неверно.
Предположим, что это сумма противоположных углов трапеции. По
третьему свойству
равнобедренной трапеции, любую
равнобедренную трапецию можно вписать в окружность, а это достижимо, когда сумма противолежащих углов равна 180° (по
свойству описанной окружности), следовательно, данное утверждение неверно.
Остается только вариант, что это углы при одном из оснований.
По
свойству равнобедренной трапеции, углы при основаниях попарно равны. По условию сумма углов равна 50°, т.е. каждый угол при одном из оснований равен 25°.
Сумма углов любого выпуклого четырехугольника равна 360°, следовательно:
360°-50°=310° - сумма углов при другом основании.
По
тому же свойству об углах равнобедренной трапеции:
310°/2=155° - углы при другом основании - это и есть бОльшие углы.
Ответ: 155
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
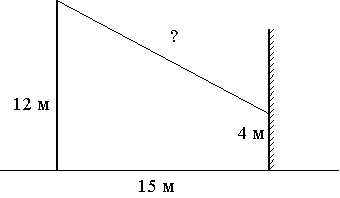От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
В прямоугольном треугольнике один из катетов равен 24, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=22.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: