
Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Рассмотрим каждое утверждение.
1) "Площадь треугольника меньше произведения двух его сторон". Площадь треугольника можно вычислить по формуле Sтреугольника=1/2*a*b*sinC, где С - угол между сторонами a и b. Т.к. значение синуса не может быть больше единицы, получается, что a*b всегда больше 1/2*a*b*sinC. Поэтому это утверждение верно.
2) "Средняя линия трапеции равна сумме её оснований" - это утверждение неверно, так как средняя линия равна полусумме оснований (по
определению).
3) "Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны". Это утверждение верно по
признаку подобия.
Ответ: 1) и 3)
Поделитесь решением
Присоединяйтесь к нам...
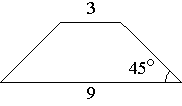 В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Стороны AC, AB, BC треугольника ABC равны 2√
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
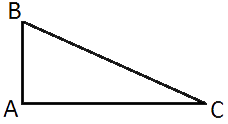 В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
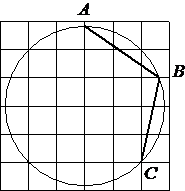 Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
Комментарии: