Площадь прямоугольного треугольника равна 128√
Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin30°=1/2 (
табличное значение)
sin30°=a/c=1/2 (по
определению синуса)
c=2a
По
теореме Пифагора:
a2+b2=c2
a2+b2=(2a)2
b2=3a2
b=a√
Из условия: Sтреугольника=ab/2=128√
a*a√
Сокращаем √
a2=128*2=256
a=16
Ответ: a=16
Поделитесь решением
Присоединяйтесь к нам...
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
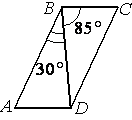Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
Сторона ромба равна 8, а расстояние от центра ромба до неё равно 2. Найдите площадь ромба.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: