
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=8, BF=15.
 ∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA=∠BAE (т.к. AE -
биссектриса).
Получается, что треугольник ABE -
равнобедренный.
BF -
биссектриса, а по
свойству равнобедренного треугольника, она так же и
медиана и
высота.
Таким образом, получается, что треугольник ABF -
прямоугольный.
По
теореме Пифагора:
AB2=AF2+BF2
AB2=82+152
AB2=64+225=289
AB=17
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
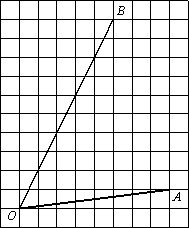 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
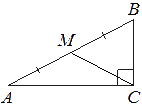 В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
Комментарии: