Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
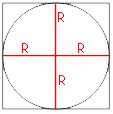Стороны
квадрата являются
касательными к окружности, следовательно, отрезок, проведенный от центра окружности к точке касания будет перпендикулярен стороне
квадрата и равен радиусу окружности (По
свойству касательной).
Получается, что сторона
квадрата равна диаметру окружности, или двум радиусам, т.е. 2*83=166
Площадь
квадрата равна произведению сторон:
S=166*166=27556
Ответ: 27556
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: