
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
Треугольник ABH
прямоугольный (т.к. AH -
высота).
Тогда cosB=BH/AB (по
определению).
AB=BC (по условию).
BC=BH+CH=48+2=50=AB
cosB=BH/AB=48/50=96/100=0,96
Ответ: 0,96
Поделитесь решением
Присоединяйтесь к нам...
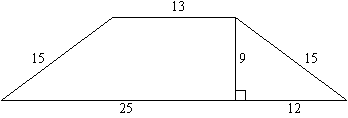 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Катеты прямоугольного треугольника равны 3√
Катеты прямоугольного треугольника равны 3√
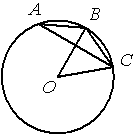 Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
 В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
В треугольнике ABC угол C равен 90°, sinA=7/17, AC=4√
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD=25.
Комментарии: