
 В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=52 и CH=13. Найдите cosB.
Треугольник ABH
прямоугольный (т.к. AH -
высота).
Тогда cosB=BH/AB (по
определению).
AB=BC (по условию).
BC=BH+CH=52+13=65=AB
cosB=BH/AB=52/65=0,8
Ответ: 0,8
Поделитесь решением
Присоединяйтесь к нам...
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 14°?
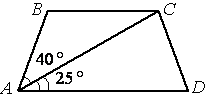 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
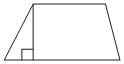 Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
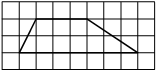 На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
На клетчатой бумаге с размером клетки 1x1 изображена трапеция. Найдите её площадь.
 Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
Комментарии: