Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
Пусть:
∠KMP=44°
∠MKP=71°
∠KPM=65°
Рассмотрим треугольник AMK.
AM=AK (по
второму свойству касательной)
Следовательно треугольник AMK -
равнобедренный, тогда, по
свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по
свойству углов на окружности).
∠KPM является
вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠KPM=65°
Применив
теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=65°+65°+∠MAK
∠MAK=50°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠KMP=44°
∠KBP=180°-44°-44°=92°
И...
∠CPM=∠CMP=∠MKP=71°
∠PCM=180°-71°-71°=38°
Ответ: 50°, 92° и 38°
Поделитесь решением
Присоединяйтесь к нам...
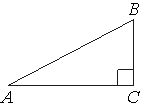В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√
В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
Основания равнобедренной трапеции равны 3 и 17, боковая сторона равна 25. Найдите длину диагонали трапеции.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: