Площадь прямоугольного треугольника равна 8√
Площадь
прямоугольного треугольника равна половине произведения катетов:
S=AC*BC/2=8√
Пусть 60-и градусам равен угол ABC.
Тангенс ABC:
td∠ABC=tg60°=AC/BC=√
BC=AC/√
S=AC*BC/2=8√
AC*BC=16√
AC*AC/√
AC2=16√
AC=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
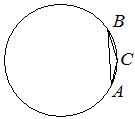В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
Найдите площадь параллелограмма, изображённого на рисунке.
Сторона равностороннего треугольника равна 18√3. Найдите радиус окружности, вписанной в этот треугольник.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-09-07 16:39:45) Администратор: Катя, с какого места решения Вам непонятно?
(2017-09-07 15:29:24) Катя: Я не поняла задачу ,можно более развернутое решение .