
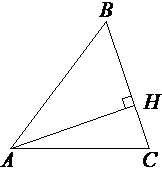
 В остроугольном треугольнике ABC высота AH равна 20√
В остроугольном треугольнике ABC высота AH равна 20√
Треугольник ABH
прямоугольный, т.к. AH -
высота.
Тогда по
теореме Пифагора:
AB2=AH2+BH2
402=(20√
1600=400*3+BH2
400=BH2
BH=20
По
определению:
cos∠B=BH/AB=20/40=1/2=0,5
Ответ: cos∠B=0,5
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
В треугольнике ABC угол C равен 90°, BC=8, AB=10. Найдите cosB.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
 В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
В треугольнике ABC известно, что ∠BAC=64°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
 Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Синус острого угла A треугольника ABC равен 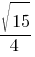 . Найдите CosA.
. Найдите CosA.
Комментарии:
(2021-12-15 15:59:07) хуесос: )))