В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=97 и BC=BM. Найдите AH.
Так как BM -
медиана, значит AM=MC=AC/2=97/2=48,5
Рассмотрим треугольник MBC.
Т.к. BC=BM (по условию задачи), значит этот треугольник
равнобедренный, BH -
высота этого треугольника. По
третьему свойству равнобедренного треугольника MH=HC=MC/2=48,5/2=24,25
Искомая AH=AC-HC=97-24,25=72,75
Ответ: AH=72,75
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
Площадь прямоугольного треугольника равна
722√
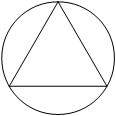Сторона равностороннего треугольника равна 2√
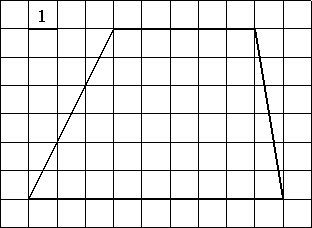Найдите площадь трапеции, изображённой на рисунке.
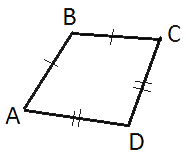В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: