
 В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Площадь
трапеции равна h*(a+b)/2, где a и b - основания трапеции, h - высота трапеции.
hтрапеции*(4+1)/2=35 (по условию задачи)
h=35/2,5=14
 Проведем
высоту треугольника ABC, как показано на рисунке.
Проведем
высоту треугольника ABC, как показано на рисунке.
hтреугольника=hтрапеции, так как они обе перпендикулярны одним и тем же параллельным основаниям трапеции и образуют прямоугольник.
Sтреугольника=hтреугольника*BC/2=14*1/2=7
Ответ: Sтреугольника=7
Поделитесь решением
Присоединяйтесь к нам...
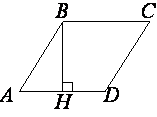 Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
| Нагреватель (котёл) | Прочее оборудование и монтаж | Средн. расход газа/ средн. потребл. мощность | Стоимость газа/электроэнергии | |
| Газовое отопление | 24 000 руб. | 18 280 руб. | 1,2 куб. м/ч | 5,6 руб./куб. м |
| Электр. отопление | 20 000 руб. | 15 000 руб. | 5,6 кВт | 3,8 руб./(кВт*ч) |
Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости устройства газового и электрического отопления?
 В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника три оси симметрии.
 Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Комментарии:
(2016-10-18 14:36:11) Администратор: настя, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-18 14:27:06) настя: дано прямоугольная трапеция авсd аd=4 ДЛИНА ВС=2 УГОЛ D=45 ГРАДУСОВ НАЙТИ ПРОЕКЦИИ ВЕКТОРОВ АD AB BC AC НА ВЕКТОР CD
(2014-05-26 13:31:53) Администратор: Коля, высота общая. Просто не всем пользователям это сразу понятно, поэтому в решении это доказывается.
(2014-05-26 10:41:11) Коля : А разве высота hтреугольника не будет общей высотой и для трапеции ?
(2014-05-25 12:50:54) Администратор: Танюшка, можно и так.
(2014-05-25 11:56:49) танюшка: Можно решить другим способом. Находим также высоту трапеции. Она равна 14. Эта же высота является высотой треугольника АСD. Находим его площадь=AD*H/2=4*14/2=28. Теперь находим площадь треугольника ABC=35-28=7
(2014-05-19 16:48:07) Администратор: Лиза, обе высоты (и трапеции, и треугольника) перпендикулярны основаниям трапеции, которые параллельны друг другу. Таким образом, высоты являются противоположными сторонами прямоугольника, поэтому они равны. Да они и не могут быть разными. Наверно, вы не правильно прочитали рисунок.
(2014-05-19 15:31:04) Лиза: Высоты не могу быть равны! Даже если по рисунку посмотреть, то высота треугольника в 2 раза меньше высоты трапеции, тк высота трапеции пересекает треугольник там, где находится средняя линия