
 В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=2/0,2=10.
Ответ: AB=10.
Поделитесь решением
Присоединяйтесь к нам...
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 14°?
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника три оси симметрии.
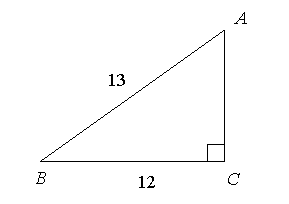 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Комментарии: