В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
По
определению синуса sinA=BC/AB => AB=BC/sinA=2/0,2=10.
Ответ: AB=10.
Поделитесь решением
Присоединяйтесь к нам...
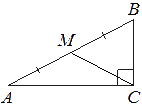В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
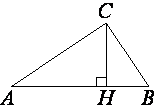В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
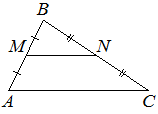Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.
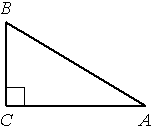В треугольнике ABC угол C прямой, BC=9, sinA=0,3. Найдите AB.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: