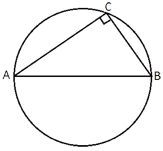
В треугольнике ABC AC=15, BC=5√
Треугольник ABC -
прямоугольный, тогда по
теореме Пифагора:
AB2=AC2+BC2
AB2=152+(5√
AB2=225+25*7
AB2=400
AB=20
Так как треугольник ABC прямоугольный, то это означает, что центр окружности находится на середине гипотенузы (по
теореме об описанной окружности).
Тогда R=AB/2=20/2=10
Ответ: R=10
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Сторона квадрата равна 9√2. Найдите диагональ этого квадрата.
Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен
60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: