
 В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Проведем дополнительный отрезок и введем обозначения как показано на рисунке:
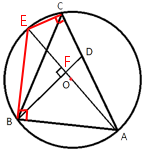 Рассмотрим треугольники AEB и AFB.
Рассмотрим треугольники AEB и AFB.
∠BAE - общий
∠EBA=90°, т.к. AE - диаметр окружности (
теорема об описанной окружности)
∠AFB=90°, т.к. по условию AD ⊥ AE
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда:
AE/AB=AB/AF => AE*AF=AB2
Рассмотрим треугольники AEC и AFD.
∠FAD - общий
∠ACE=90°, т.к. AE - диаметр окружности (
теорема об описанной окружности)
∠AFD=90°, т.к. по условию BD ⊥ AE
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда:
AE/AD=AC/AF => AD=AE*AF/AC
Подставляем выше найденное равенство:
AD=AB2/AC=322/64=16
CD=AC-AD=64-16=48
Ответ: CD=48
Поделитесь решением
Присоединяйтесь к нам...
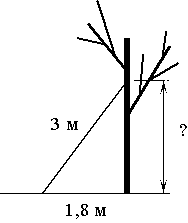 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Синус острого угла A треугольника ABC равен 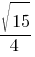 . Найдите CosA.
. Найдите CosA.
 В треугольнике ABC угол C равен 45°, AB=6√
В треугольнике ABC угол C равен 45°, AB=6√
Стороны AC, AB, BC треугольника ABC равны 2√
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Комментарии:
(2017-05-20 00:10:22) Администратор: Alissa, да, это опечатка, спасибо, что обнаружили. Исправлено!
(2017-05-19 19:24:30) Alissa: В решении задачи есть такая запись\"∠AFB=90°, т.к. по условию AD ⊥ AE\". Почему \"AD ⊥ AE\"?У вас опечатка \"ВD ⊥ AE\"
(2017-05-17 22:39:41) Администратор: Лера, АЕ - это диаметр окружности, следовательно любой вписанный угол, который опирается на АЕ будет прямым. Поэтому ЕВ всегда будет перпендикулярен АВ.
(2017-05-17 21:33:21) Лера: Если начертить другой треугольник, то перпендикуляры из точки Е не будут опускаться в точку В, значит так задача не решится
(2017-02-01 15:25:29) Администратор: Ася, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-31 18:01:19) Ася: В треугольниках ABE и KMP известны стороны: AB=3,BE=5,AE=7.MP=15,PK=21 нАЙДИТЕ ДЛИНУ СТОРОНЫ mk ЕСЛИ угол P= углу E